Early on in the development of MadStone, we thought it would be cool if the play field looked like a castle wall made of stone blocks. There should be blocks of different sizes and shapes, and all of the blocks should look like they fit together, no matter what shape the overall structure took on.
Sounds easy enough, right? If MadStone was built in a 3d engine, this would have been done for us, but MadStone is entirely a 2D game. The challenge here was making a set of completely 2d blocks look like they fit together in 3 dimensions.
Originally, the blocks didn’t overlap at all. This was easy, but there was no depth to the blocks.
When the blocks don’t overlap at all, you can draw them in any order and it looks the same.
Second, we had a version where the blocks overlapped vertically, but not horizontally. We accomplished this by drawing the blocks bottom to top, so that the higher blocks would draw on top of the lower ones, making it look like they fit together. All together, it ended up looking sort of like a wall, but more like a bunch of independent columns.
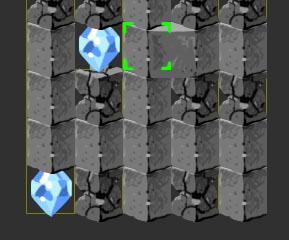
So finally on our third iteration of the blocks, we took that idea one step further. But because the blocks had to overlap vertically and horizontally, we could no longer use the same bottom-to-top right-to-left algorithm as before. There were two main problems with it.
First, because some blocks are larger than 1×1, our old algorithm which looped through each grid square right to left and bottom to top would draw larger blocks more than once. This is a problem because it ruins the intended draw order. Luckily, the fix isn’t too hard. Before the draw loop begins, we set up a 2D array of boolean values, representing each square of the entire grid. Every time an object drew, it would flip all of its corresponding squares in the 2d boolean grid to true, meaning that the square had already draw once. If the loop reached a square that was marked true in the boolean array, the loop would skip over that square and continue.
That solved problem one, but there was still another issue. In this next picture, you can see how blocks that were 2 squares tall vertically sometimes drew behind blocks to their upper-right. Unfortunately, the simple drawing loop with the 2d boolean array we had here was too simple to get the wall of blocks to all draw in the correct order.

There were also more complicated situations that led to similar problems. Luckily, a solution did exist (Jacob gets credit for coming up with the algorithm). Here is the basic idea of how it works.
First we set up a nested loop, but this one is a little different than before. Instead of the outer loop being bottom-to-top and the inner loop being right-to-left, we have the outer loop iterating right-to-left and the inner loop iterating top-to-bottom. I’ll explain why this is necessary in a second. Also like before, we needed to use the 2d array of drawn squares to make sure that large objects only draw once. But here’s where it really gets interesting.
Instead of simply drawing an object when the draw loop encounters it, the drawing code instead makes a call to a recursive function that says, essentially, “draw what’s below you first (right to left), and then draw yourself.” Here’s an example of execution:
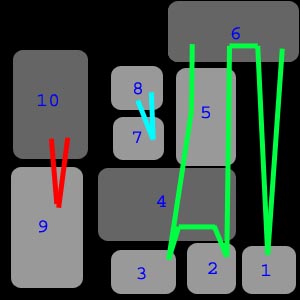
In this crude drawing, imagine the grey square are blocks. The blue numbers on each block represent the order that they draw. The crazy lines show the order in which the blocks are visited by the recursion. Basically, we start the nested draw loops by looking at the block in the upper right corner (the block labelled ‘6’). This block makes a recursive call, starting on the right side, and following the green line down to block 1. There is nothing below block 1, so it draws, and the function call returns to block 6.
Now block 6 makes the recursive call to the square below its left hand side. Block 5 asks block 4 to draw, which asks block 2 to draw. There is nothing below block 2, so it draws, and the call returns to block 4. Like before, block 4 goes down its left hand side, and block 3 draws. With nothing else below it, block 4 draws, the call returns to block 5, and block 5 draws. Finally, the recursive call returns to block 6 (where it started originally), and block 6 draws. From just this first set of recursive calls, we’ve already drawn most of the blocks.
Having finished block 6, the draw loop scans the rest of the top row, and there is nothing more to draw. Continuing down to the 2nd row from the right, block 5 is ignored (the 2d boolean array has already marked it as drawn), and we encounter block 8. Block 8 tells block 7 to draw, which tells block 4 to draw. But since 4 has already drawn, the call returns to 7, which draws, and 8, which draws.
Finally, the loop advances past block 8 and hits block 10. Block 10 asks block 9 to draw. It does, and the call returns to block 10, which draws. There! We’ve drawn all 10 blocks in the correct order. Now we have something that looks like this:

The algorithm might seem complicated, and it is at first glance. After all, you’re dealing with two nested for loops, a recursive call that is potentially invoked more than once per block, and a 2d array of booleans that has to be passed around to keep track of it all. But the implementation actually isn’t too bad, once you’ve got the algorithm.
And there you have it: a 3d wall of blocks drawing in 2d.



